베이즈 정리를 설명하기 전 배경 지식
조건부 확률(conditional probability) : 주어진 사건이 일어난 상태에서, 다른 사건이 일어날 확률
- 주어진 사건이 일어날 확률을 p(F)라고 할 때, 다른 사건 E가 일어날 확률은 p(E | F) 이다. (E occurs given that F occurs)
- 조건부 확률 공식 (p(F) > 0) 으로 부터 베이즈 정리 유도
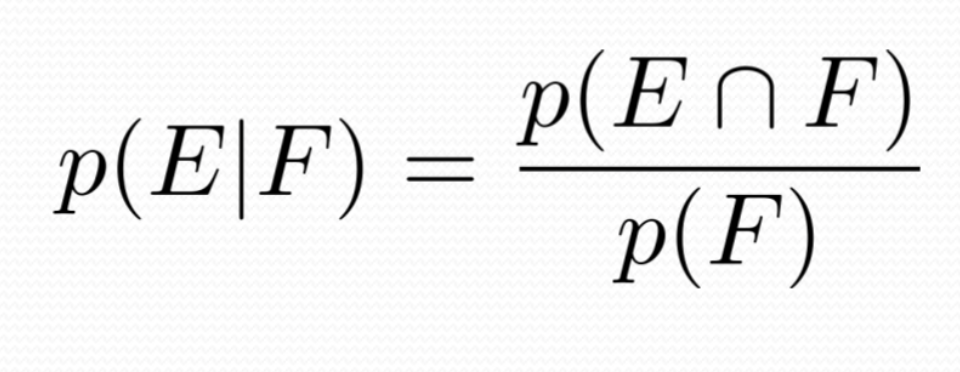
- 이 정의에 의해서 p(E) > 0 일때, 아래의 식도 도출해 낼 수 있다.

- 두 식에 있는 분모를 이항하면, 아래의 식을 도출해 낼 수 있다.

- p( E ∩ F ) 라는 값을 가지고 있기 때문에 두 식을 같다고 할 수 있다. ( Equating the two formula for p( E ∩ F ) shows that, )

- 이 값을 p(F) 혹은 p(E)로 나누면 아래의 식이 나온다.

- E 는 E와 전체집합과의 교집합, S = F ∪ ~F

and

-조건부 확률의 정의에 의해 (by the definition of conditional probability)

- 베이즈 정리의 공식이 도출된다. ( 위의 공식의 p(E)를 p(F | E) 공식에 대입하면 아래 식이 나옴 )

베이즈 정리 ( Bayes' theorem )
Suppose that E and F are events from a sample space S such that p(E) ≠ 0 and p(F) ≠ 0. Then

베이즈 정리 적용 (Applying bayes's theorem)
문제 ) 100,000명 사람 중 1명이 특정 질병이 있다. 두가지 테스트가 있는데, 첫째는 병이 있는 사람에게 병이 있다고 99%로 맞출 수 있는 테스트고 둘째는 병이 없는 사람에게 병이 없다고 95%로 맞출 수 있는 테스트이다.
(Suppose that one person in 100,000 has a particular disease. There is a test for the disease that gives a positive result 99% of the time when given to someone with the disease. When given to someone without the disease, 99.5% of the time it gives a negative result)
a) 병 있는 사람 맞출 확률 the probability that a person who test positive has the disease.
b) 병 없는 사람 맞출 확률 the probability that a person who test negative does not have the disease.
solution)
D는 그 사람에게 병이 있다는 사건 D be the event that the person has the disease
▷ ~D는 그 사람에게 병이 없다는 사건 D be the event that the person has not the disease
E는 그 사람이 병이 있다고 테스트 되는 사건 E be the event that this person tests positive.
▷ ~E는 그 사람이 병이 없다고 테스트 되는 사건 E be the event that this person tests negative.
a) 테스트 해봤는데 병 있는 사람 맞출 확률 the probability that a person who test positive has the disease.



b) 테스트 해봤는데 병 없는 사람 맞출 확률 the probability that a person who test negative does not have the disease.


결론 : 테스트 해봤는데 병 있는 사람 맞출 확률은 2%, 테스트 해봤는데 병 없는 사람 맞출 확률99.9%임
the number of false positive of people diagnostic test is far greater than the number of true positive.
So, people who test positive for the disease should not be ovrely concerned that they actually have disease
베이즈 정리 표준화 ( Gereralized Bayes' theorem)

- E가 표준 집합 S에 속한 이벤트이고 F(i)가 n만큼 합집합이 될때 서로 독립적이어서 F(i)를 다더하면 S라면, 이 식이 성립한다.

Bayesian Spam Filters
어떻게 우리는 스팸메세지를 구분할 수 있을까? How do we develop a tool for determining whether an email is likely to be spam?
Spam filter을 이용해 앞으로 올 메세지가 스팸메시지인지 예측할 수 있다. We can use this information along with Bayes’ law to predict the probability that a new email message is spam.
과정
1. 스팸 메시지의 집합 : B , 스팸 메시지가 아닌 것의 집합 : G 로 설정

2. 특정한 단어 w를 포함한 메일이 스팸 메시지일 확률 Estimated probability that an email containing w is spam

3. 특정한 단어 w를 포함한 메일이 스팸 메세지가 아닐 확률 Estimated probability that an email containing w is not spam

4. S를 spam 메시지가 도착한 사건, E를 메세지가 w라는 단어를 포함하는 사건이라고 가정
Suppose S be the event that the message is spam, and E be the event that the message contains the word w.
5. w라는 단어를 포함하는 메세지가 spam메시지일 확률

6.스팸이거나 스팸이 아닐 확률은 모두 0.5 (1/2) 임 -> spam message 빈도에 대한 data가 있다면 그것을 사용해서 더 좋은 측정을 할 수 있다.
Assuming that it is equally likely that an arbitrary message is spam and is not spam; i.e., p(S) = ½ .
-> If we have data on the frequency of spam messages, we can obtain a better estimate for p(s).
7. 분자 분모에 모두 P(S) 와 P(~S)가 있으므로 약분한다.

8. spam메세지에 대한 최종식

- r(w) 메시지가 스팸인지 측정 estimates the probability that the message is spam.
- p(w) 메시지가 스팸일 때, w라는 단어가 포함되는 확률 means message contains the word w given that the message is spam.
- q(w) 메시지가 스팸이 아닐 때, w라는 단어가 포함되는 확률 means message contains the word w given that the messsage is not spam.
Bayesian Spam Filters 에 대한 적용
문제) Rolex라는 단어가 들어간 메시지는 2000개 중에 250개가 스팸이다. 그리고 1000개 중에 5개가 스팸이 아니다. 앞으로 들어오는 메시지가 스팸일 확률은? threshold 가 0.9일 때, 스팸메시지를 막을 수 있을까?
We find that the word “Rolex” occurs in 250 out of 2000 spam messages and occurs in 5 out of 1000 non-spam messages. Estimate the probability that an incoming message is spam. Suppose our threshold for rejecting the email is 0.9.
solution)
1. 메시지가 스팸일 확률

2.메시지가 스팸이 아닐 확률

3.계산

4. r(Rolex)가 0.9보다 크기 때문에, threshold를 0.9로 설정하면 스팸메시지를 막을 수 있다.
Because r(Rolex) is greater than the threshold 0.9, we reject such messages as spam
여러개의 단어 spam filtering (Bayesian Spam Filters using Multiple Words)
- 1개 이상의 단어로 spam filtering 을 하면 정확도가 올라간다.
Accuracy can be improved by considering more than one word as evidence.
- E1 : word w1를 포함하는 사건 E2: word w2를 포함하는 사건
Consider the case where E1 and E2 denote the events that the message contains the words w1 and w2 respectively
- 이 두개의 사건은 독립적이다.

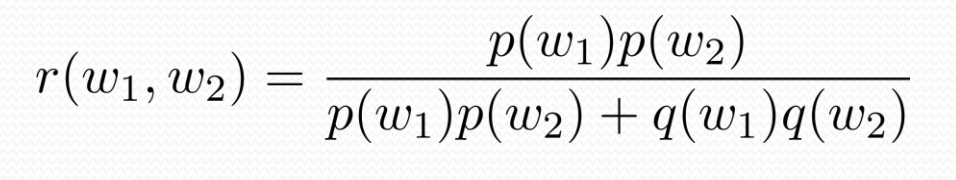
Bayesian Spam Filters using Multiple Words 적용
문제) 2000개의 스팸과 1000개의 non-스팸메시지가 있다. "stock"이라는 단어는 400개의 스팸과 60개의 non-spam을 발생시킨다. "undervalued"라는 단어는 200개의 스팸과 25개의 non-spam을 발생시킨다. 두 단어가 들어간 메시지가 스팸일 확률은 ? threshold 가 0.9일 때, 스팸메시지를 막을 수 있을까?
We have 2000 spam messages and 1000 non-spam messages. The word “stock” occurs 400 times in the spam messages and 60 times in the non-spam. The word “undervalued” occurs in 200 spam messages and 25 non-spam.
solution)
1. stock 이 들어간 메시지가 스팸일 확률, 아닐 확률

2. undervalued가 들어간 메시지가 스팸일 확률, 아닐 확률

3. 식과 풀이

Because we have set the threshold for rejecting message at 0.9, such messages will be rejected by the filter.
더 많은 단어를 test할수록, spam filter는 더 정확해진다.the more words we consider, the more accurate the spam filter.
multiple word 표준화


We can further improve the filter by considering pairs of words as a single block or certain types of strings.
'ੈ✩‧₊˚Computer Science > 이산수학' 카테고리의 다른 글
| 동치관계(equivalence relation)/동치류(Equivalence Class) (0) | 2020.11.29 |
|---|---|
| 관계의 표현(representing relations) (0) | 2020.11.25 |
| 관계(Relations) / 관계의 특징(Relations and their properties) (0) | 2020.11.24 |


