행렬로 표현
유한 집합 사이의 관계는 1-0 행렬로 표현 가능하다. A relation between finite sets can be represented using a zero-one matrix.

예제) 관계 R = {(2,1), (3,1),(3,2)} 일때 행렬로 표현해보기 (a,b) 임
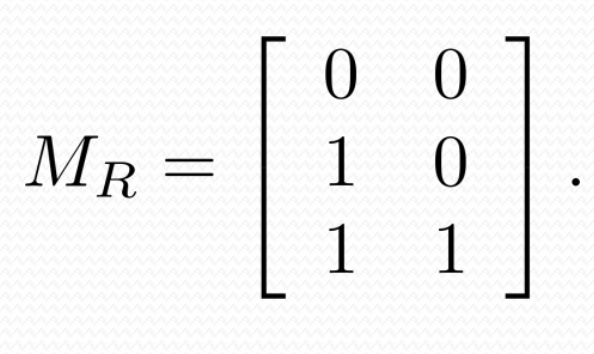
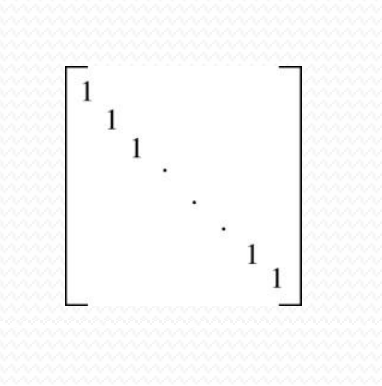
반사관계(reflective relation)일 때의 행렬 : 대각선이 모두 1이다. diagonal is all 1
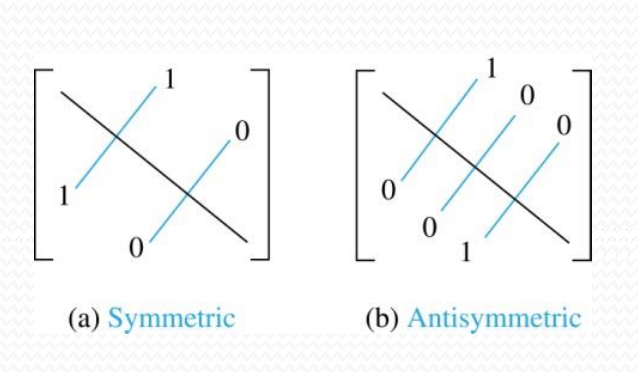
대칭관계(symmetric relation)일 때의 행렬 : m(i,j)와 m(j,i)가 모두 1 혹은 m(i,j)와 m(j,i)가 모두 0
반대칭관계(antisymmetric relation)일 때의 행렬 : m(i,j)와 m(j,i)가 다르기 때문에 동시에 1인 경우 빼고 다됨
방향 그래프(directed graph)
: consists of a set V of vertices (or nodes) together with a set E of ordered pairs of elements of V called edges (or arcs).
-(a,a)를 표현하는 선은 루프이다. An edge of the form (a,a) is called a loop.
예시) (a, b), (a, d), (b, b), (b, d), (c, a), (c, b), (d, b) 를 방향그래프로 표현하기 (verticles : a,b,c,d)
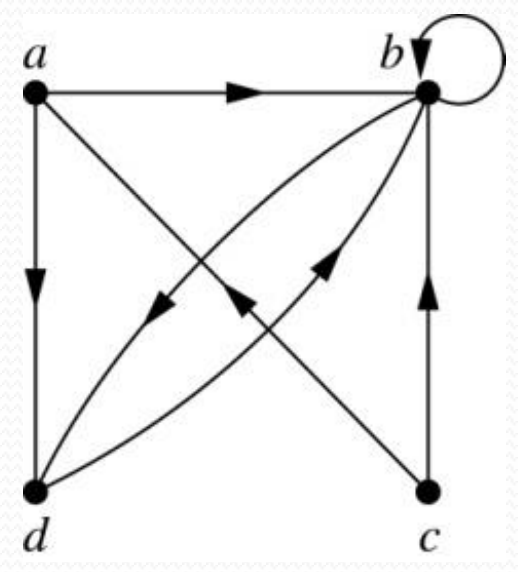
예시) 이 그래프의 좌표는 ?
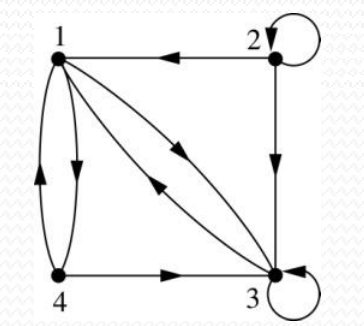
답 ) R={(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,3),(4,1),(4,3)}
방향 그래프로도 관계 특징을 설정할 수 있다.
reflective : 꼭짓점에 모든 원소에 대한 루프가 있을 때
symmetric : (x,y)에 대한 edge가 있을 때, (y,x)에 대한 edge도 있을 때
antysymmetric : (x,y)에 대한 edge가 있고, x!=y일 때 (y,x)는 없다.
transivity : (x,y)에 대한 edge가 있고, (y,z)에 대한 edge도 있을 때 (x,z)에 대한 edge가 있어야함
'ੈ✩‧₊˚Computer Science > 이산수학' 카테고리의 다른 글
| 동치관계(equivalence relation)/동치류(Equivalence Class) (0) | 2020.11.29 |
|---|---|
| 관계(Relations) / 관계의 특징(Relations and their properties) (0) | 2020.11.24 |
| 베이즈 정리(Bayes' theorem) (0) | 2020.11.21 |


